Terrace Steps on Platinum (111) Surface.

Introduction.

This tutorial demonstrates two different approaches to creating terrace steps on platinum surfaces, based on the work presented in the following manuscript:

Manuscript

Šljivančanin, Ž., & Hammer, B., "Oxygen dissociation at close-packed Pt terraces, Pt steps, and Ag-covered Pt steps studied with density functional theory." Surface Science, 515(1), 235–244. DOI: 10.1016/s0039-6028(02)01908-8. ¹

We will focus on creating platinum surface with terrace steps, as shown in FIG. 1. B:

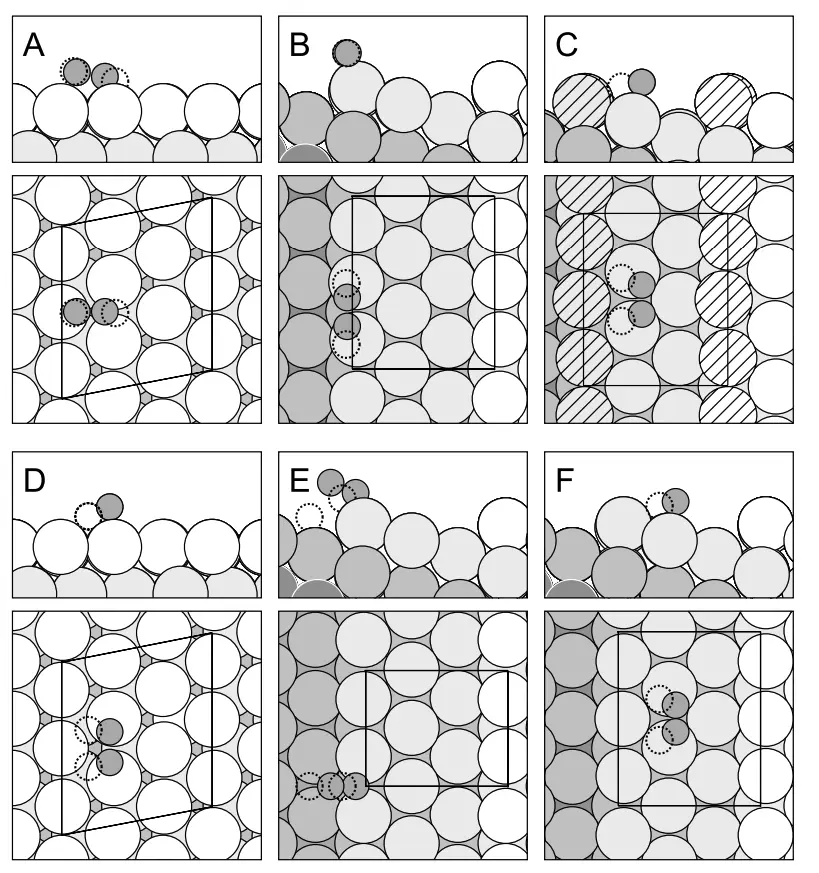
We will demonstrate two methods:

1. Creating a Pt(211) surface which inherently contains steps
2. Creating a terrace step on a Pt(111) surface using the TerraceSlabDefectBuilder

1. Method I: Create Pt(211) Surface.

• Creates a surface with inherent steps
• Smaller unit cell
• Fixed step geometry
• Good for studying specific crystal faces

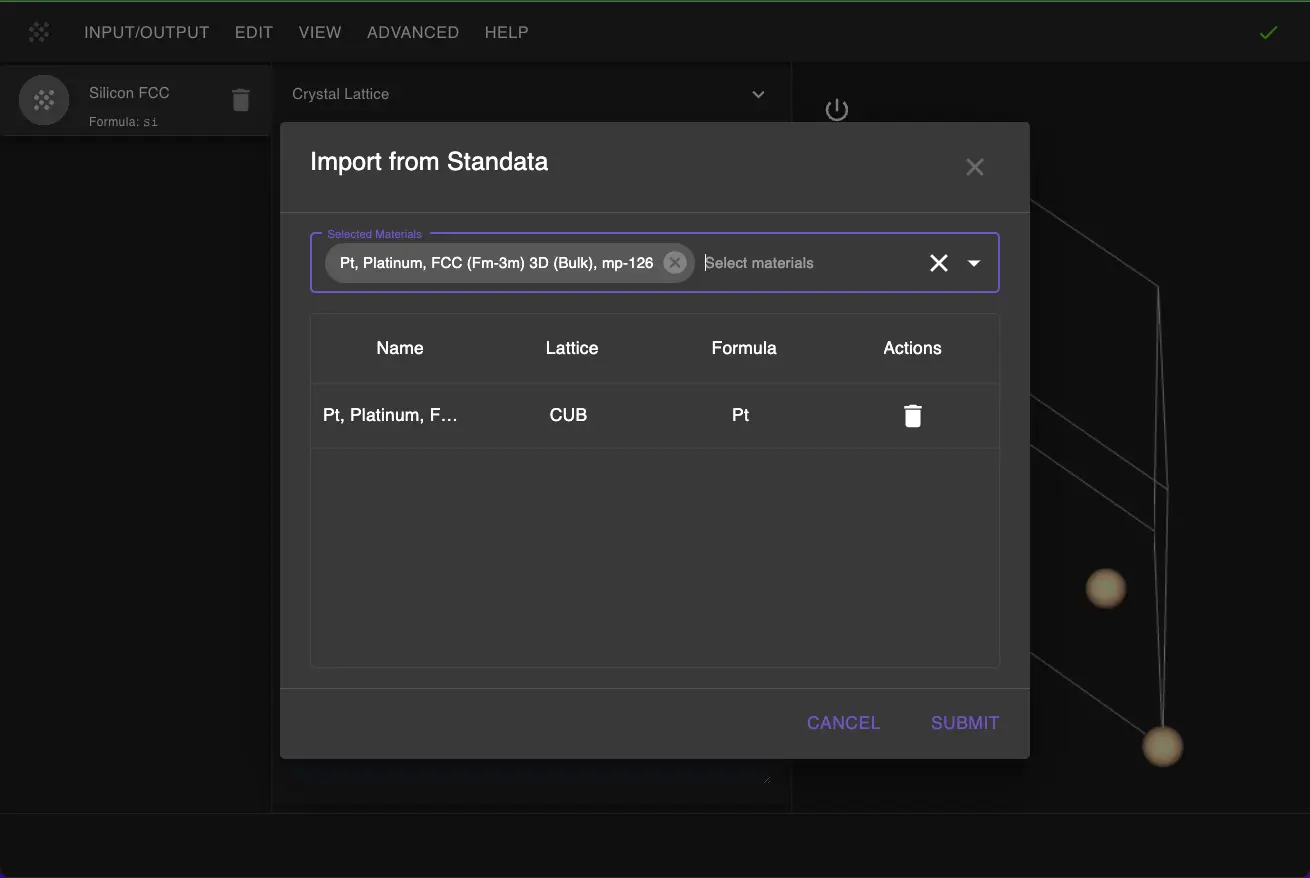
1.1. Import Base Material.

First, we need to import the platinum material from Standata:

1. Navigate to Materials Designer
2. Click on "Input/Output" menu
3. Select "Import from Standata"
4. Search for "Pt" and select the bulk platinum material

1.2. Launch JupyterLite Environment.

Select "Advanced > JupyterLite Transformation" to open JupyterLite.

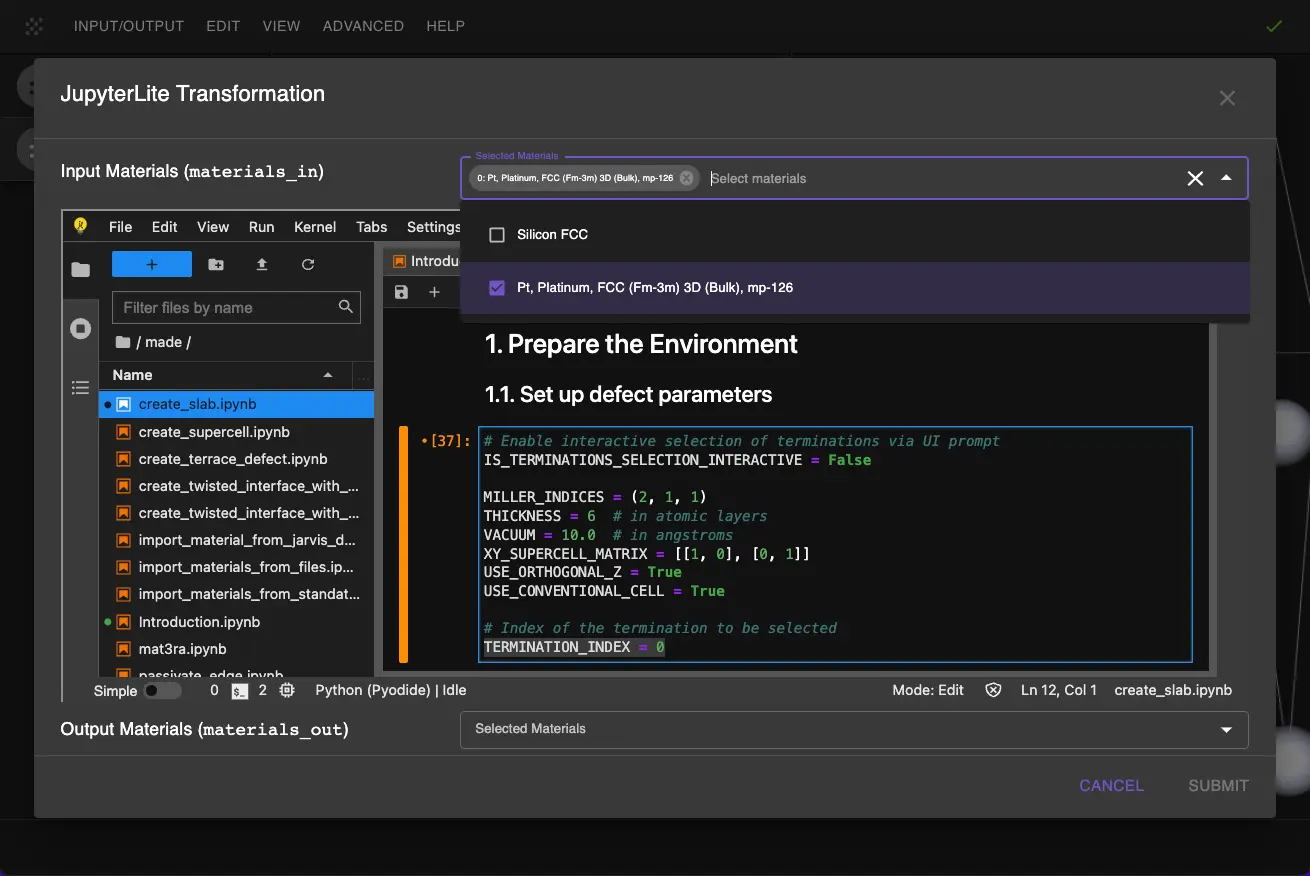
1.3. Configure Slab Parameters.

Open a create_slab.ipynb notebook and set up the slab parameters in the "1.1. Set up notebook" cell:

MATERIAL_NAME = "Pt"
MILLER_INDICES = (2, 1, 1)
THICKNESS = 6  # in atomic layers
VACUUM = 10.0  # in angstroms
XY_SUPERCELL_MATRIX = [[1, 0], [0, 1]]
USE_ORTHOGONAL_Z = True
USE_CONVENTIONAL_CELL = True
TERMINATION_INDEX = 0

These parameters will create a Pt(211) surface with:

• 6 atomic layers thickness
• 10 Å vacuum region
• Orthogonal z-axis
• Using the conventional unit cell

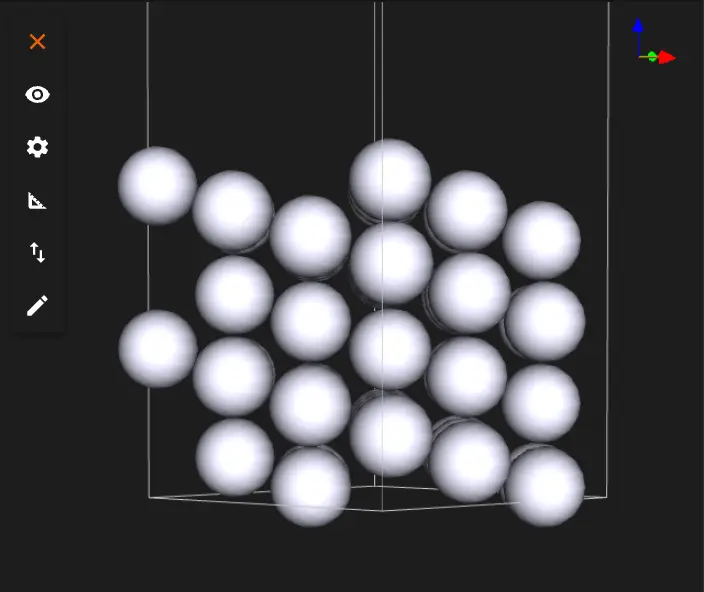
1.4. Create the Slab.

Run the notebook by clicking Run > Run All in the top menu. The notebook will generate the Pt(211) surface.

2. Method II: Create Terrace Step Defect on Pt(111).

• More flexible control over step placement
• Larger surface area available
• Customizable terrace height
• Better for complex step arrangements

2.1. Open Terrace Defect Notebook.

First, open create_terrace_defect.ipynband select Pt as the input material.

2.2. Configure Terrace Parameters.

CUT_DIRECTION = [0, 1, 1] -- Normal vector for cutting plane, which will give a perfect periodic match along x and a match along y after rotation. DEFAULT_SLAB_PARAMETERS["miller_indices"] = (1, 1, 1) -- Miller indices for Pt(111) surface DEFAULT_SLAB_PARAMETERS["xy_supercell_matrix"] = [[2, 0], [0, 2]] -- Supercell matrix for final structure (which will effectively control the size of the terrace)

# Material selection
# Which material to use from input list
MATERIAL_INDEX = 0  

# Terrace parameters:
# Normal vector describing a plane that cuts the terrace from added layers (Miller indices)
CUT_DIRECTION = [0,1,1]  
# Point the cutting plane passes through, in crystal coordinates
PIVOT_COORDINATE = [0.5, 0.5, 0.5] 
# Height of terrace in atomic layers
NUMBER_OF_ADDED_LAYERS = 1  
# Use cartesian instead of crystal coordinates
USE_CARTESIAN_COORDINATES = False  
# Rotate to match periodic boundary conditions
ROTATE_TO_MATCH_PBC = True  

# Slab parameters for creating a new slab if provided material is not a slab
DEFAULT_SLAB_PARAMETERS = {
    "miller_indices": (1,1,1),
    "thickness": 6,
    "vacuum": 10.0,
    "use_orthogonal_z": True,
    "xy_supercell_matrix": [[2, 0], [0, 2]]
}

# Visualization parameters
SHOW_INTERMEDIATE_STEPS = True
# Structure repeat in view
CELL_REPETITIONS_FOR_VISUALIZATION = [1, 1, 1]  

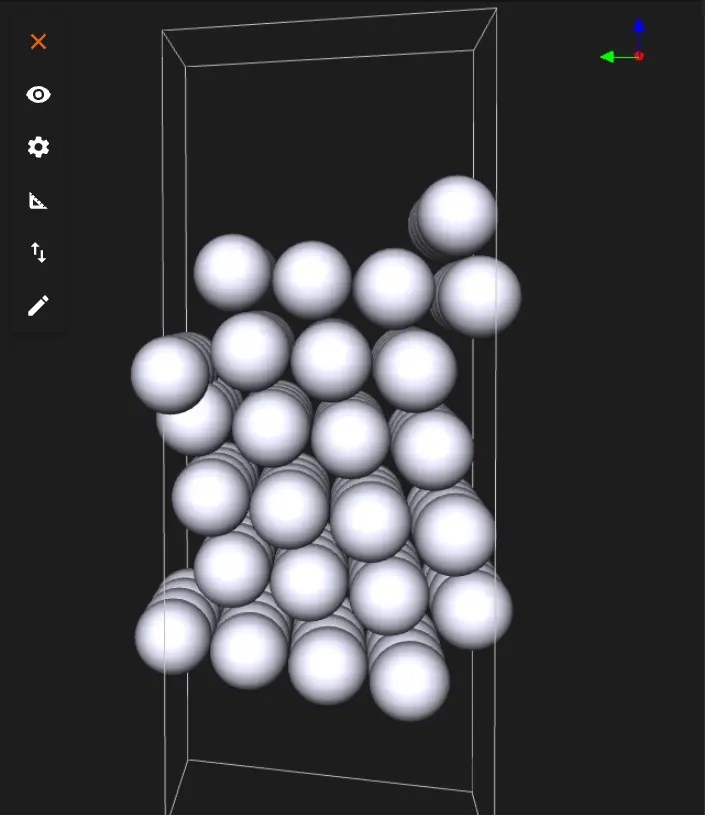
2.3. Create the Terrace.

Run the notebook to create the Pt(111) surface with a terrace step.

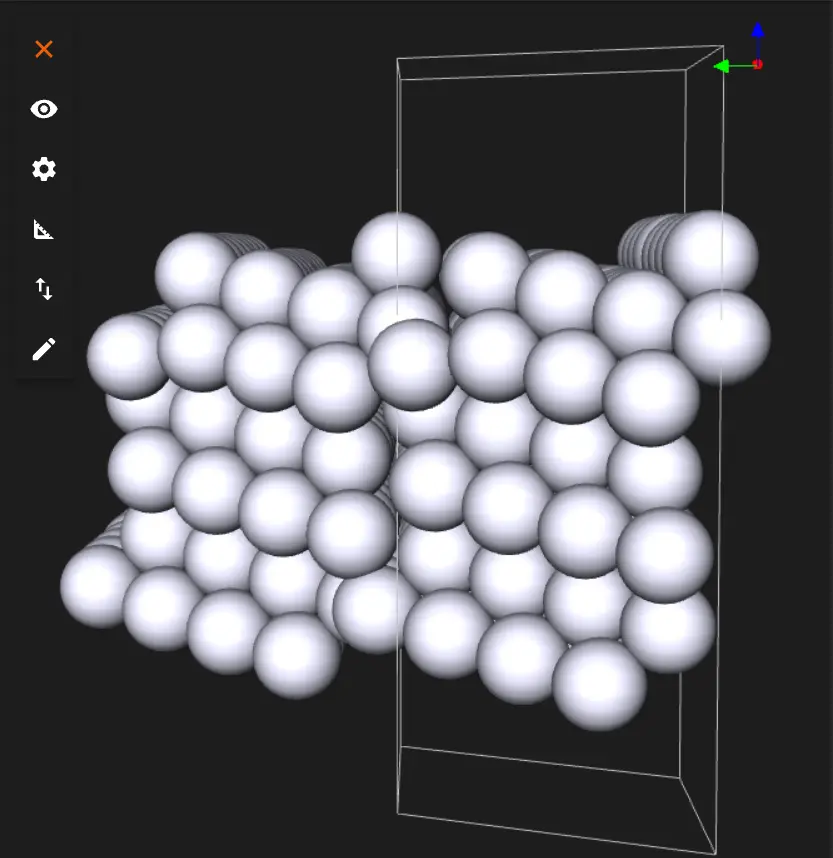
The same material with repetitions:

The user can save or download the material in Material JSON format or POSCAR format.

Interactive JupyterLite Notebook.

The following JupyterLite notebook demonstrates both approaches. Select "Run" > "Run All Cells" to execute the notebook.

⛶ Full Screen

References.

---

1. Z. Šljivančanin and B. Hammer. Oxygen dissociation at close-packed Pt terraces, Pt steps, and Ag-covered Pt steps studied with density functional theory. Surface Science, 515(1):235–244, 2002. URL: https://doi.org/10.1016/s0039-6028(02)01908-8. ↩