Ripple perturbation of a Graphene sheet.

Introduction.

This tutorial demonstrates the process of creating edge induced ripples in graphene nanosheet based on the work presented in the following manuscript, where the mechanical properties of graphene edges were studied.

Manuscript

Thompson-Flagg, R. C., Moura, M. J. B., & Marder, M. "Rippling of graphene" EPL (Europhysics Letters), 85(4), 46002 (2009) DOI: 10.1209/0295-5075/85/46002. ¹²³

We will focus on creating graphene with edge-induced ripples that match the patterns observed in experimental studies, as shown in FIG. 1.

1. Create Graphene Nanoribbon.

1.1. Load Graphene Material.

Navigate to Materials Designer and import the graphene material from the Standata.

1.2. Launch JupyterLite Session.

Select the "Advanced > JupyterLite Transformation" menu item to launch the JupyterLite environment.

1.3. Open create_nanoribbon.ipynb notebook.

Find create_nanoribbon.ipynb in the list of notebooks and click/double-click to open it.

1.4. Set up nanoribbon parameters.

Edit notebook to set the nanoribbon parameters:

# Widths and lengths are in number of unit cells
WIDTH = 40
VACUUM_WIDTH = 10
LENGTH = 40
VACUUM_LENGTH = 10
EDGE_TYPE = "zigzag"  # "zigzag" or "armchair"

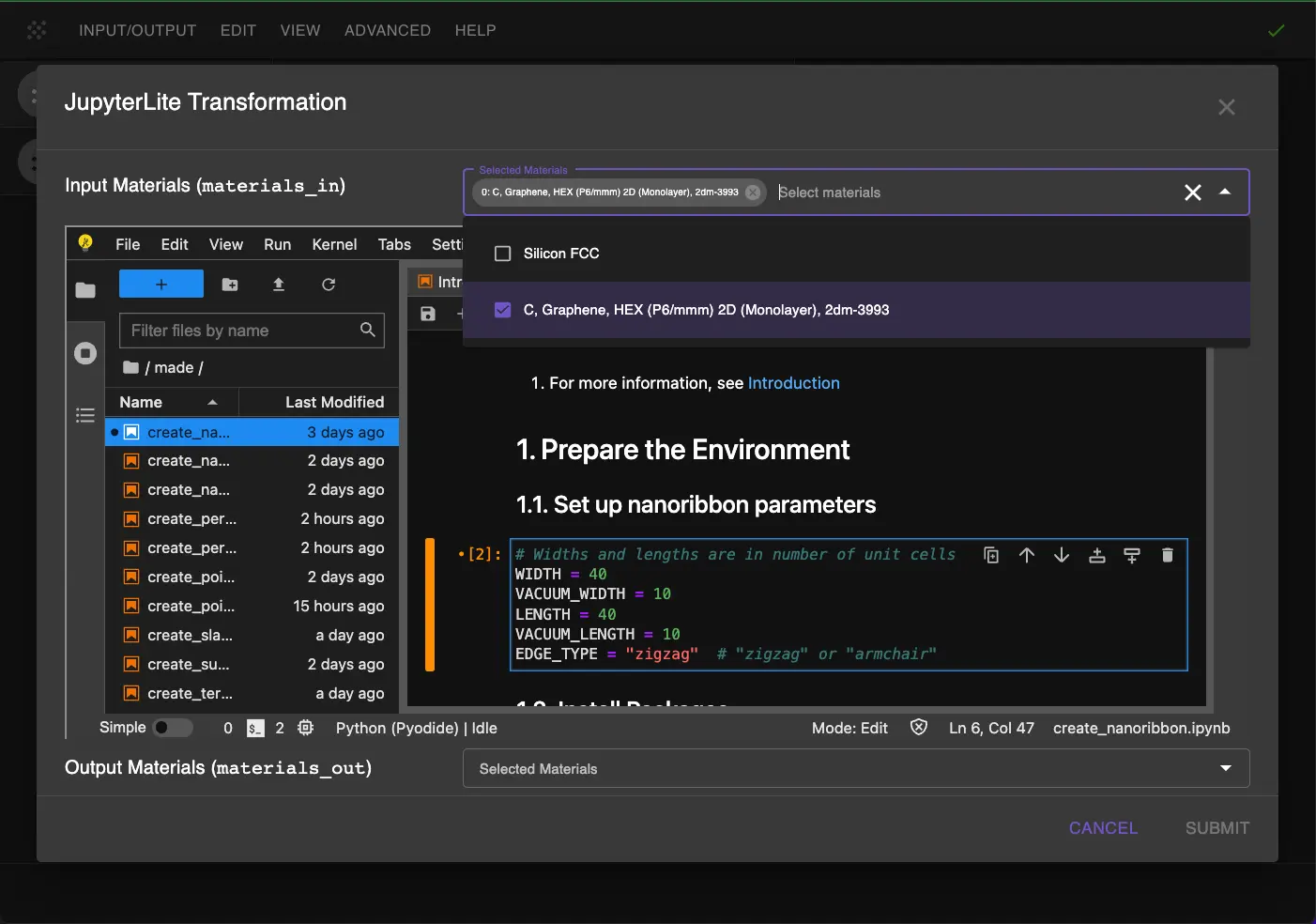
1.5. Run the notebook.

After setting the parameters, run the notebook by selecting "Run > Run All Cells" from the menu. This will create a graphene nanoribbon with the specified dimensions.

2. Create Ripples in the Nanoribbon.

2.1. Open create_perturbation_custom.ipynb notebook.

Find create_perturbation_custom.ipynb in the list of notebooks and click/double-click to open it.

2.2. Set up perturbation parameters.

Next, we need to set up the parameters for creating rippled graphene.

Edit notebook in 1.2. to set generic perturbation parameters:

# Set whether to preserve geodesic distance and scale the cell accordingly to match PBC
PRESERVE_GEODESIC_DISTANCE = False

# Set whether to use Cartesian coordinates for the perturbation function
USE_CARTESIAN_COORDINATES = False
MATERIAL_NAME = "Graphene"

Then modify section 1.3 to define the custom perturbation function:

import sympy as sp

# Variables for the perturbation function (for SymPy)
variable_names = ["x", "y", "z"]
x, y, z = sp.symbols(variable_names)

# Set the parameters for the perturbation function
AMPLITUDE = 0.09  # Ripple amplitude
WAVELENGTH = 0.2  # Wavelength of ripples
EDGE_WIDTH = 0.25  # Width of edge effect
PHASE_X = 0.0  # Phase shift for x direction
PHASE_Y = sp.pi/2  # Phase shift for y direction

# Create edge masks for both x and y using polynomial functions
left_edge_x = sp.Max(0, (EDGE_WIDTH - x) / EDGE_WIDTH)
right_edge_x = sp.Max(0, (x - (1 - EDGE_WIDTH)) / EDGE_WIDTH)
left_edge_y = sp.Max(0, (EDGE_WIDTH - y) / EDGE_WIDTH)
right_edge_y = sp.Max(0, (y - (1 - EDGE_WIDTH)) / EDGE_WIDTH)

# Combine edge masks
edge_mask_x = left_edge_x + right_edge_x
edge_mask_y = left_edge_y + right_edge_y
edge_mask = edge_mask_x + edge_mask_y

# Wave pattern
wave_pattern = (
    sp.sin(2 * sp.pi * x / WAVELENGTH + PHASE_X) * 
    sp.sin(2 * sp.pi * y / WAVELENGTH + PHASE_Y)
)

# Combine waves with edge mask
custom_sympy_function = AMPLITUDE * wave_pattern * edge_mask

Key parameters explained:

• AMPLITUDE Controls the height of the ripples (0.09 Å)
• WAVELENGTH Controls the spacing between ripples (0.2 in crystal coordinates)
• EDGE_WIDTH Controls how far the ripples extend from the edges (0.25 in crystal coordinates)
• PHASE_X/PHASE_Y Controls the phase shift of the ripple pattern

2.3. Run the notebook.

After setting the parameters, run the notebook by selecting "Run > Run All Cells" from the menu.

3. Pass the Material to Materials Designer.

The rippled graphene structure will be automatically passed back to the current Materials Designer environment where user can save it.

Graphene with edge-induced ripples with amplitude of 0.09 crystal units.

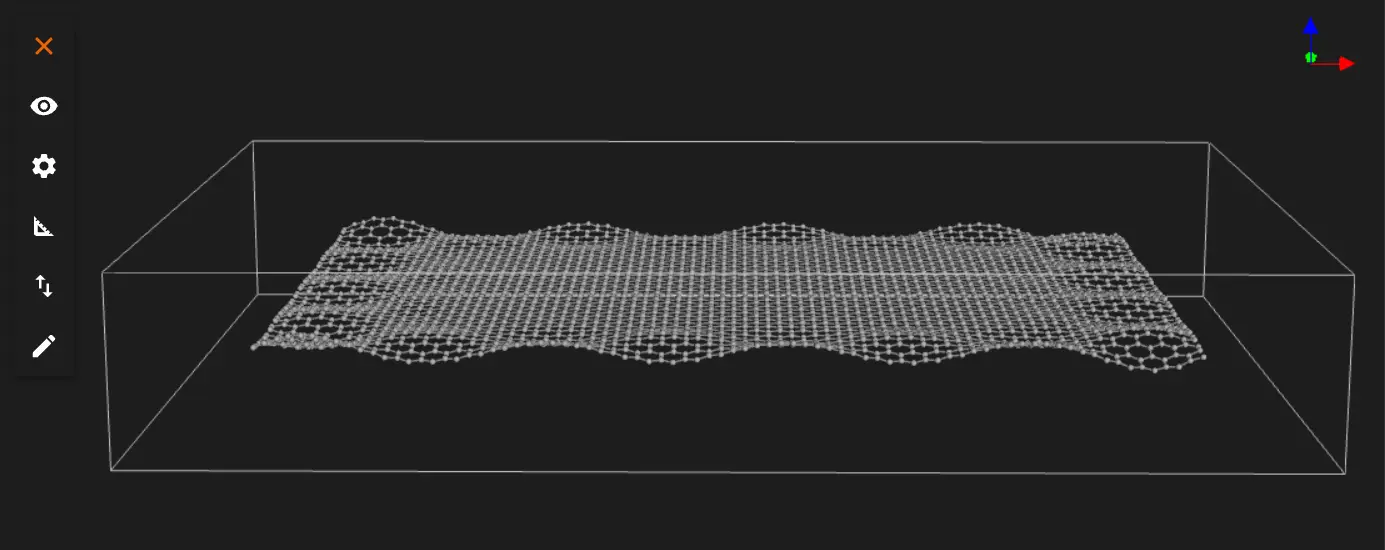
Graphene with edge-induced ripples with amplitude of 0.27 crystal units.

Or user can save or download the material in Material JSON format or POSCAR format.

Interactive JupyterLite Notebook.

The following JupyterLite notebook demonstrates the process of creating rippled graphene. Select "Run" > "Run All Cells".

⛶ Full Screen

Parameters Fine-tuning.

If user need to adjust the ripple pattern, user can modify these key parameters:

1. To change ripple height:

2. Adjust AMPLITUDE (higher value = taller ripples)

3. To change ripple spacing:

4. Adjust WAVELENGTH (higher value = more spread out ripples)

5. To change how far ripples extend from edges:

6. Adjust EDGE_WIDTH (higher value = ripples extend further from edges)

7. To change the ripple pattern:

8. Adjust PHASE_X and PHASE_Y to modify the wave interference pattern

References.

---

1. R. C. Thompson-Flagg, M. J. B. Moura, and M. Marder. Rippling of graphene. EPL (Europhysics Letters), 85(4):46002, 2009. URL: https://doi.org/10.1209/0295-5075/85/46002. ↩

2. A. Fasolino, J. H. Los, and M. I. Katsnelson. Intrinsic ripples in graphene. Nature Materials, 6:858–861, 2007. URL: https://doi.org/10.1038/nmat2011. ↩

3. L. A. Openov and A. I. Podlivaev. Interaction of the stone-wales defects in graphene. Physics of the Solid State, 52(1):2010, 2010. URL: https://doi.org/10.1134/S1063783415070240. ↩